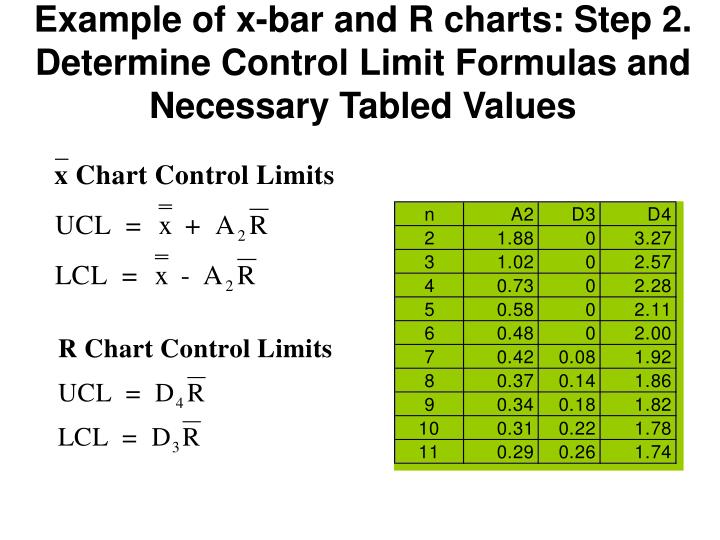
bionwatcher.blogg.se - Xbar and r chart example

#XBAR AND R CHART EXAMPLE PDF#

The R-chart plots the average range and the limits of the range. This demonstrates the centering of the subset values. Future experimental subsets are plotted compared to these values. The X-Bar chart displays the centerline, which is calculated using the grand average, and the upper and lower control limits, which are calculated using the average range. X-Bar (average) charts and R (range) -charts are often paired together. An x-bar chart is often paired with either an r-chart or an s-chart to give a complete picture of the same set of data. There are three types of control charts used determine if data is out of control, x-bar charts, r-charts and s-charts. That is, n/N <= 0.05 where n is the sample size and N is the population size. Alternatively, if the population is finite but the sample size is less than 5% of the population size, we can still approximate the population to be near infinite.

Finally, the population size, N is assumed to be infinite.

If it drifts monthly you might set your subset to be 24 hours or 12 hours. If you know that your sensor has the tendency to drift every day, you might select a 30 minute subset of data. For example, if you were using a pH sensor, the sensor would most likely output pages of data daily.

The subsets are defined, based on the data and the process.

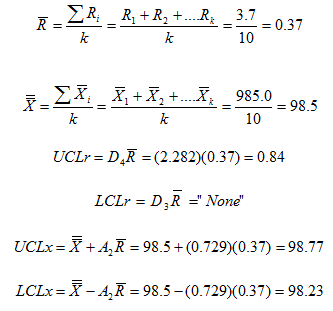
It is assumed that the first occurrence of a point not falling within the predicted limits shows that the system must be unstable since it has changed from the predictive model. This is because any point taken should fall within the statistical predictions. Future data taken to determine process stability can be of any size.The upper and lower control limits for the process can then be determined from this data.

The average range is simply the average of subset ranges. The average standard deviation is simply the average of subset standard deviations. The grand average is the average of all subset averages.

From these subsets, a grand average, an average standard deviation, and an average range are calculated.

A subset average, subset standard deviation, and subset range will be computed for each subset. The number of subsets is represented as k.

Multiple subsets of data must be collected, where a subset is simply a set of n measurements taken over a specific time range.

Because future process quality will be compared to these predictions, they must be based off of a data set that is taken while the operation is running properly.

The initial predictions for the process must be made while the process is assumed to be stable.

There are a few key conditions that must be met when constructing control charts: For more on six-sigma control, see six sigma. These rules are discussed in greater detail later in this section.Ĭontrol Charts are commonly used in six sigma control today, as a means of overall process improvement. In generalized terms, if data points fall within three standard deviations of the mean (within the red lines), the process is considered to be in control. The centerline is the mean value of the data set and the green, blue and red lines represent one, two, and three standard deviations from the mean value.

#XBAR AND R CHART EXAMPLE PDF#

The image below shows the control chart for a data set with the PDF overlay. For example, if an engineer knows the mean (grand average) value, standard deviation, and range of a process, this information can be displayed as a bell curve, or population density function (PDF). Control charts build on this basic idea of statistical analysis by plotting the mean or range of subsequent data against time. For good and safe control, subsequent data collected should fall within three standard deviations of the mean.

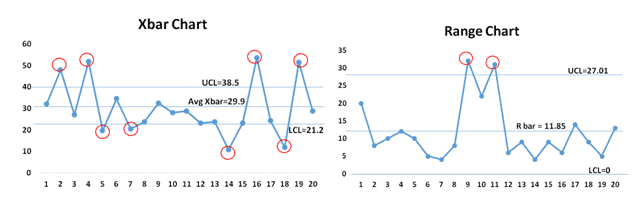
Then, subsequent data can be compared to this already calculated mean, standard deviation and range to determine whether the new data fall within acceptable bounds. The boundaries for these classifications are set by calculating the mean, standard deviation, and range of a set of process data collected when the process is under stable operation. \)Ī process may either be classified as in control or out of control.